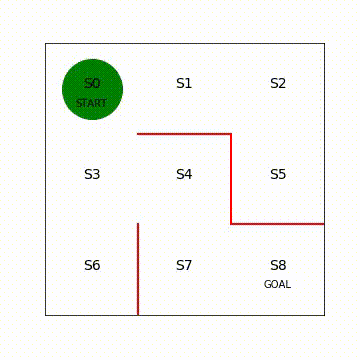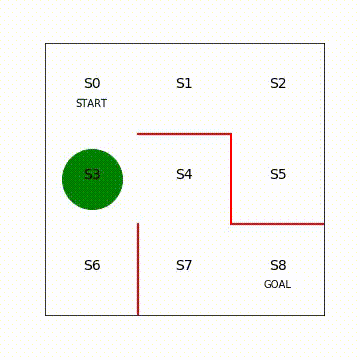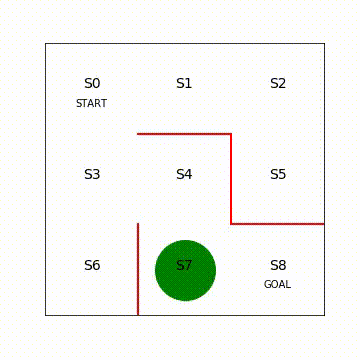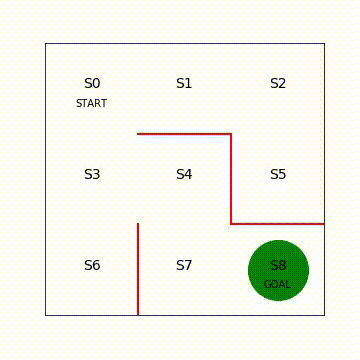
计算每个状态下 执行某一动作的概率
将最初的概率表更新
直到概率表的变化微乎其微时终止
从而得到最优路线
这里介绍以下softmax函数:
特征对概率的影响是乘性的
假设有一个数组V,Vi表示V中的第i个元素,那么这个元素的softmax数值为:
$$
S_{i}=\frac{e^{i}}{\sum_{j} e^{j}}
$$
价值迭代(马尔科夫决策过程)
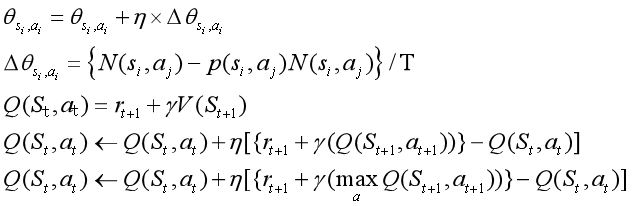
Q学习和sarsa学习的区别参考以上公式
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inlinefig = plt.figure(figsize = (5,5))
ax = plt.gca()
plt.plot([1,1],[0,1],color = 'red',linewidth=2)
plt.plot([1,2],[2,2],color = 'red',linewidth=2)
plt.plot([2,2],[2,1],color = 'red',linewidth=2)
plt.plot([2,3],[1,1],color = 'red',linewidth=2)
plt.text(0.5,2.5,'s0',size = 14,ha = 'center')
plt.text(1.5,2.5,'s1',size = 14,ha = 'center')
plt.text(2.5,2.5,'s2',size = 14,ha = 'center')
plt.text(0.5,1.5,'s3',size = 14,ha = 'center')
plt.text(1.5,1.5,'s4',size = 14,ha = 'center')
plt.text(2.5,1.5,'s5',size = 14,ha = 'center')
plt.text(0.5,0.5,'s6',size = 14,ha = 'center')
plt.text(1.5,0.5,'s7',size = 14,ha = 'center')
plt.text(2.5,0.5,'s8',size = 14,ha = 'center')
plt.text(0.5,2.3,'Start',ha = 'center')
plt.text(2.5,0.3,'goal',ha = 'center')
ax.set_xlim(0,3)
ax.set_ylim(0,3)
plt.tick_params(axis='both',which='both',bottom='off',top='off',labelbottom='off',right='off',left='off',labelleft='off')
line, = ax.plot([0.5],[2.5],marker="o",color="g",markersize=60)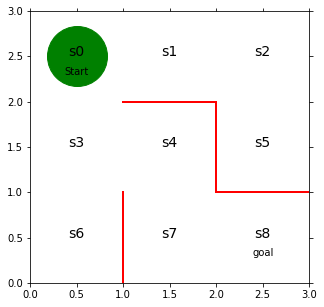
theta_0 = np.array([[np.nan,1,1,np.nan],
[np.nan,1,np.nan,1],
[np.nan,np.nan,1,1],
[1,1,1,np.nan],
[np.nan,np.nan,1,1],
[1,np.nan,np.nan,np.nan],
[1,np.nan,np.nan,np.nan],
[1,1,np.nan,np.nan]])def softmax_convert_into_pi_from_theta(theta):
beta = 1.0 #beta为逆温度(日语) beta的数值越小则行动越random随机
[m,n] = theta.shape
pi = np.zeros((m,n))
exp_theta = np.exp(beta * theta)
for i in range(0,m):
pi[i,:] = exp_theta[i,:]/np.nansum(exp_theta[i,:])
pi = np.nan_to_num(pi)
return pipi_0 = softmax_convert_into_pi_from_theta(theta_0)
print(pi_0)softmax函数计算中 np.nansum()中nan的数值忽略,不放入计算
[[0. 0.5 0.5 0. ]
[0. 0.5 0. 0.5 ]
[0. 0. 0.5 0.5 ]
[0.33333333 0.33333333 0.33333333 0. ]
[0. 0. 0.5 0.5 ]
[1. 0. 0. 0. ]
[1. 0. 0. 0. ]
[0.5 0.5 0. 0. ]]
def get_action_and_next_s(pi,s):
direction = ["up","right","down","left"]
next_direction = np.random.choice(direction,p = pi[s,:])
if next_direction == "up":
action = 0
s_next = s-3
elif next_direction == "right":
action = 1
s_next = s+1
elif next_direction == "down":
action = 2
s_next = s+3
elif next_direction == "left":
action = 3
s_next = s-1
return [action,s_next]def goal_maze_ret_s_a(pi):
s = 0
s_a_history = [[0,np.nan]]
while(1):
[action,next_s] = get_action_and_next_s(pi,s)
s_a_history[-1][1] = action
# [-1]是表示最后一行
s_a_history.append([next_s,np.nan])
if next_s == 8:
break
else:
s = next_s
#注意缩进
return s_a_historys_a_history = goal_maze_ret_s_a(pi_0)
print(s_a_history)
print("迷路问题结局需要step:" + str(len(s_a_history)-1))[[0, 2], [3, 2], [6, 0], [3, 0], [0, 1],
[1, 3], [0, 1], [1, 1], [2, 3], [1, 1],
[2, 3], [1, 1], [2, 2], [5, 0], [2, 3],
[1, 3], [0, 1], [1, 3], [0, 1], [1, 1],
[2, 3], [1, 3], [0, 2], [3, 1], [4, 2],
[7, 1], [8, nan]]
迷路问题结局需要step:26
def update_theta(theta,pi,s_a_history):
eta = 0.1
T = len(s_a_history)-1
[m,n] = theta.shape
delta_theta = theta.copy()
for i in range(0,m):
for j in range(0,n):
if not (np.isnan(theta[i,j])):
# i状态下的操作取出? 数组SA[]括号里只有一个数字的时候代表行?
# 列表推导式 [表达式 for 变量 in 列表]
# [表达式 for 变量 in 列表 if 条件]
SA_i = [SA for SA in s_a_history if SA[0] == i]
# i 状态下的动作j执行次数 是SA 不是SA[0]
SA_ij = [SA for SA in s_a_history if SA == [i,j]]
N_i = len(SA_i)
N_ij = len(SA_ij)
delta_theta[i,j] = (N_ij - pi[i,j]*N_i)/T
new_theta = theta + eta * delta_theta
return new_theta
new_theta = update_theta(theta_0, pi_0, s_a_history)
pi = softmax_convert_into_pi_from_theta(new_theta)
print(pi)[[0. 0.50192307 0.49807693 0. ]
[0. 0.5 0. 0.5 ]
[0. 0. 0.49711542 0.50288458]
[0.33333333 0.33333333 0.33333333 0. ]
[0. 0. 0.50096154 0.49903846]
[1. 0. 0. 0. ]
[1. 0. 0. 0. ]
[0.49903846 0.50096154 0. 0. ]]
stop_epsilon = 10**-4
theta = theta_0
pi = pi_0
is_continue = True
count = 1
while is_continue:
s_a_history = goal_maze_ret_s_a(pi)
new_theta = update_theta(theta,pi,s_a_history)
new_pi = softmax_convert_into_pi_from_theta(new_theta)
# 方策 pi的变化输出 np.abs 差值的绝对值
print(np.sum(np.abs(new_pi - pi)))
print("迷路问题解决需要step:" + str(len(s_a_history)-1))
# 在这里当方案pi的变化非常小的时候 这里设定为小数点4位后终止
if np.sum(np.abs(new_pi - pi)) < stop_epsilon:
is_continue = False
else:
theta = new_theta
pi = new_pi
0.009063800389401577
迷路问题解决需要step:38
0.02818744894750541
优化过程步进行运算次数很多这里省略
.
.
.
0.0004803718650859268
迷路问题解决需要step:4
0.00047881784079845113
迷路问题解决需要step:4
0.0004772712904493638
迷路问题解决需要step:4
0.0004757321664344491
迷路问题解决需要step:4
0.0022237054467947846
迷路问题解决需要step:6
0.00047977332401702433
迷路问题解决需要step:4
0.0004782214782191284
迷路问题解决需要step:4
0.0004766770960367636
迷路问题解决需要step:4
0.00047514012992791455
迷路问题解决需要step:4
0.0004736105327279652
迷路问题解决需要step:4
0.00047208825764356865
迷路问题解决需要step:4
0.0004705732582512903
迷路问题解决需要step:4
0.00046906548849294863
迷路问题解决需要step:4
0.0004675649026737866
迷路问题解决需要step:4
0.0004660714554580933
迷路问题解决需要step:4
0.0004645851018637709
迷路问题解决需要step:4
0.00046310579726372564
迷路问题解决需要step:4
0.00046163349737722917
迷路问题解决需要step:4
0.0022164095549151615
迷路问题解决需要step:6
0.002469026834838472
迷路问题解决需要step:6
0.0004725170614619835
迷路问题解决需要step:4
0.0004709960188524001
迷路问题解决需要step:4
.
.
.
迷路问题解决需要step:4
0.00010171860551497561
迷路问题解决需要step:4
0.00010156167609453107
迷路问题解决需要step:4
0.00010140511295706964
迷路问题解决需要step:4
0.0010352497734007326
迷路问题解决需要step:6
0.0001026577982205408
.
.
.
0.00010000526452905167
迷路问题解决需要step:4
9.985247147614555e-05
迷路问题解决需要step:4里设定的终止值是在10**-4以下
途虽然已经找到最优路线4step,偶尔也会走其他路线6step
# 有效数字保留3位 不显示指数
np.set_printoptions(precision = 3,suppress = True)
print(pi)[[0. 0.012 0.988 0. ]
[0. 0.31 0. 0.69 ]
[0. 0. 0.403 0.597]
[0.009 0.98 0.011 0. ]
[0. 0. 0.985 0.015]
[1. 0. 0. 0. ]
[1. 0. 0. 0. ]
[0.018 0.982 0. 0. ]]
from matplotlib import animation
from IPython.display import HTML
# IPython这是是大写
def init():
line.set_data([],[])
return (line,)
def animate(i):
state = s_a_history[i][0]
x = ((state%3)+0.5)
y = 2.5 - int(state/3)
line.set_data(x,y)
return (line,)
anim = animation.FuncAnimation(fig,animate,init_func = init,frames = len(s_a_history),interval = 200,repeat = False)
HTML(anim.to_jshtml())